Olivine-wadsleyite transition in (Mg,Fe)2SiO4
Introduction
D410 and Ol-Wd transition
- Abrupt increase of seismic wave velocities near 410 km depth
-
- D410
- observed by many seismologists
- A key to understand the Earth’s mantle
- D410 <= Ol-Wd transition in (Mg,Fe)2SiO4
-
- phase relation has to be precisely determined!
Previous study
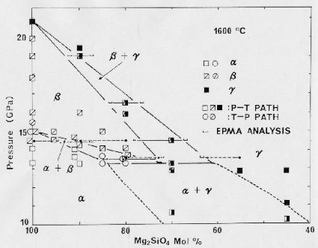
- Katsura & Ito [1989]
-
- Quench method by a Kawai-type high-pressure apparatus
- (Mg,Fe)2SiO4 binary system
At 1200 and 1600 ºC - Precise compositional measurement by EPMA
- pressures are not precise
This study
- Phase relation of the binary (Mg,Fe)2SiO4 system
-
- In situ X-ray diffraction
-
- Pressure determination by MgO scale
- Compositional measurement
-
- quench products using an electron microprobe
- At 1600 and 1900 K
Experimental Procedure
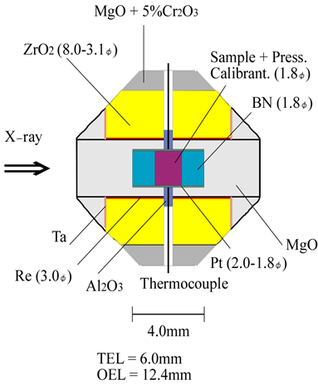
Cell assembly
- Furnace
-
- Cylindrical Re heater
- ZrO2 thermal insulating sleeve
- MgO sample container
- Pt tubular sample capsule
- BN X-ray window
- T measurement
-
- W3Re-W25Re TC
- Measured on the sample capsule
- X-rays
-
- parallel to the furnace axis
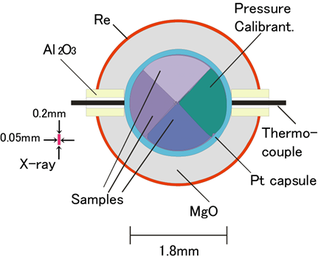
Sample
- Synthetic olivine solid solutions (MgxFe1-x)2SiO4
-
- x = 0.97, 0.95, 0.93, 0.90, 0.85, 0.80 and 0.70
- Column shape, sintered at 1670 K with H2:CO2 = 1:1
- Ground into sub-columns with pie-shaped cross section
- 3 or 4 separate solutions could be loaded together into a Pt tube with a pressure marker
Fitting of the experimental results
- Formalism given by Stixrude [1997]
-
- xa, xb :Fe2SiO4 contents of olivine and wadsleyite
- PMg, PFe: Transition pressures of the end menbers
- K = xa(1- xb)/ xb(1- xa): partition coefficient
- Π=(P - PFe )/(PMg - PFe): normalized pressure
- xa = (1 - K1- Π)/(1 - K) , xb = (KΠ - 1)/(1 - K)
- 1900 K:
-
- K = 0.61, PMg = 14.6 GPa, PFe = 5.7 GPa
- 1600 K:
-
- K = 0.47, PMg = 13.0 GPa, PFe = 4.2 GPa
Results
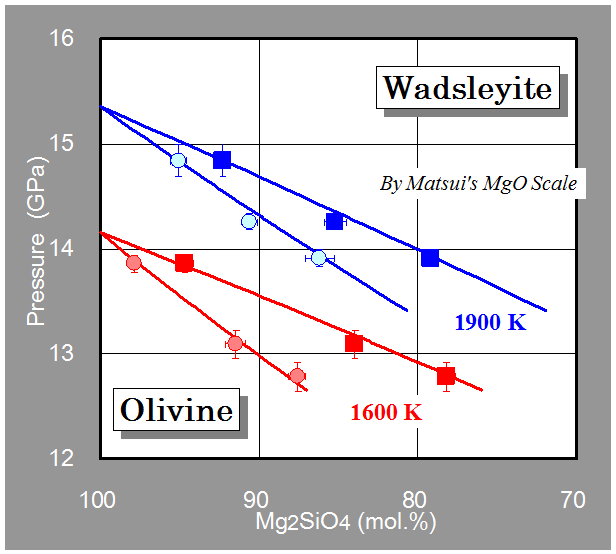
Discussion
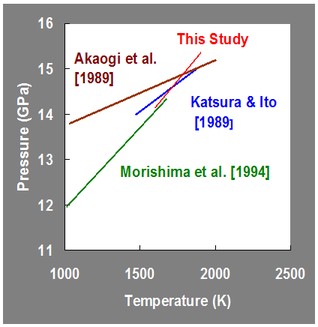
Comparison with previous studies
- Mg2SiO4 end member
-
- Generally consistent with the previous studies
- agree with the low-T data given by Morishima et al. [1994]
- Steeper gradient (4.0 MPa/K) than those of the quench experiment [Katsura and Ito, 1989] (2.5 MPa/K) and thermochemical calculation [Akaogi et al., 1989].
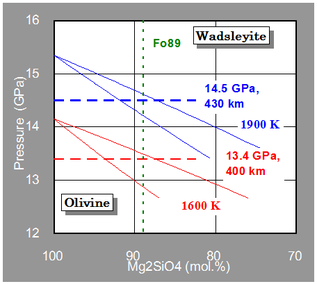
Temperature Estimation
- Discontinuity Depth <=> Transition Pressure -> Temperature
- Pressure of points with Ol/Wa=1:2 at Fo89 composition
-
- 1600 K: 13.4 GPa, 400 km
- 1900 K: 14.5 GPa, 430 km
- 3.7 MPa/K, 0.1 km/K
Temperature at D410
- Assuming a pyrolite bulk rock composition
-
- Flanagan & Shearer (1999):
-
- 418km -> 14.06 GPa -> 1770K
- Gu et al. (1998):
-
- 411 km -> 13.81 GPa -> 1710 K
- Revenaugh & Jordan (1991):
-
- 414 km -> 13.92 GPa -> 1740K
- Uncertainty of the MgO EoS: 0.15~0.17 GPa
- 1760±45 K
- It is impossible to assume much higher temperatures
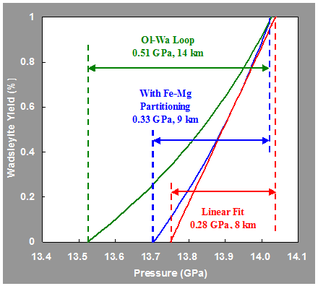
Thickness of the 410-km discontinuity
- Thickness of Ol-Wa loop at 1740 K in a pyrolite mantle
-
- 0.51 GPa, 14 km
- Thickness is decreased due to Fe-Mg partitioning among the mantle minerals [Irifune & Isshiki, 1998]
-
- 0.33 GPa, 9km
- Large effect
- The effective thickness is smaller due to non-linearity of yielding rate of the phase transition [Stixrude, 1997]
-
- 0.28 GPa, 8km
- Small effect
5-km thickness of the 410-km discontinuity is difficult to explain!
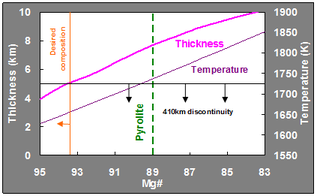
Effect of bulk composition: Large Mg#
- Pyrolite: Mg# = 89.
- In order to obtain 5-km thickness, Mg# should be higher than 93.
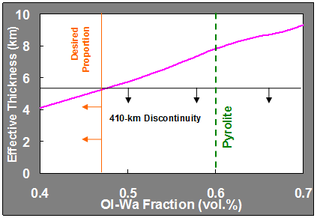
Effect of bulk composition: olivine fraction
- Small Ol/Wa fraction
Pyrolite: Ol/Wa 60 vol.% - if the olivine fraction is less than 50 %, we can obtain the thickness less than 5 km.
Conclusion
- The comparison of the discontinuity depth with the transition pressure gives T= 1760 K at 410 km depth.
-
- Note: this temperature was revised by Katsura et al. [2010]
- In order to explain the thin D-410, the olivine fraction could be smaller than usually considered or Mg# could be higher than usually considered.
