Grüneisen parameter
The Grüneisen parameter [Wiki], γth, is defined as a change in P by a change in density of E at constant V. Namely,
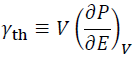
(1)
To put it plainly, γth is the ratio of thermal pressure to thermal energy [Wiki]. Or, it describes how much P increases when the matter is heated.
It is expressed by:

(2)
If γth is defined by this equation, it is called the thermodynamic Grüneisen parameter.
To put it plainly, what Eq (2) means is as follows.
- If E increases, the matter wants to increase its V due to α, because T should increase with E increase. Therefore, γth is proportional to α.
- If KT is higher, the potential V increase that the E increase wants to causes larger P increase. Accordingly, γth is proportional to KT.
- If the CV is larger, T increase becomes smaller for a given E increase, and therefore, γth is inversely proportional to CV.
In the case of MgSiO3 bridgmanite at ambient conditions, α = 2.0×10-5 K-1, KT = 260×109 Pa, V = 24×10-6 m3 mol-1, CV is 80 J K-1 mol-1, and therefore, γth = 1.1.
Note that γth is a dimensionless parameter.
Eq. (2) is obtained from Eq. (1) by the following way.

(3)
The numerator of Eq (3) is:

(4)
The denominator of Eq (3) is:
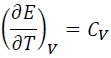
(5)
Using Eqs (3)-(5), Eq. (2) is obtained from Eq. (1) as:
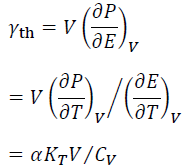
(6)
The definition of the Grüneisen parameter, Eq. (1), is the Mie-Grüneisen EOS [Wiki] itself:

(7)
There are other ways to define the Grüneisen parameter.
For example, the mode Grüneisen parameter, γi, is defined as:
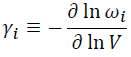
(8)
where ωi is the angular frequency of the lattice vibration of the mode i.
The Debye gamma, γD, is defined as:
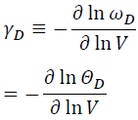
(9)
where ωD is the Debye cut-off (angular) frequency [Wiki], and ΘD is the Debye temperature [Wiki].
We will discuss the mode Grüneisen parameter and Debye gamma elsewhere.
